微信号：weixin888
?原来，数学不好的时候，真的很难深入下去做研究。最近的两个月时间里，我就边学习SOCP相关的理论知识，一边拿它当工具来分析多视角几何中的问题（包括Triangulation,Homography Estimation等）。接触到SOCP的起因在于大多多视觉几何下面的问题通常可以通过建立优化模型来求解，而凸优化又是这类模型中性质最为优良的一种——它具有全局最优值（因而也是大家研究最多的一种模型）。不例外，有关Triangulation,Homography Estimation的问题都能很好的利用SOCP模型来拟合求解，这相关的基础性研究工作在Hartley （1995），Fredrik Kahl（2007）等人发表的论文中都有很好的体现。我作为一个炮灰级的研究者，担任的工作也仅是站在巨人们的肩膀上，在现有的确定性参数模型上添加一个扰动集（用p范数来限定），把原问题变作一个不确定性优化问题，企图借助鲁棒优化的思想，把模型的适用空间进一步的泛化，使我们算法在复杂环境下的鲁棒性更好，抗噪性更强。
研究中，我自认为自己最缺乏的就是没有系统的学习过优化知识，于是，自己搜遍手头上能找到的与优化相关的资料，到目前为止，基本熟悉线性和非线性优化，凸优化，鲁棒优化等基础概念，以及单纯形算法、内点法、梯度法、牛顿迭代法及LM迭代法等从局部或全局角度求解优化问题的搜索算法，建立了基本的数学优化知识框架。其中，感触最深的莫过于对二阶锥规划（SOCP）的学习。先贴出关于SOCP概念上定义的图：
? 
这里一定要注意，当你确定要用SEDUMI软件来求解你的SOCP模型时，sedumi(A,b,c,k)中的参数并不是依照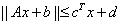
中的参数来设定，而是要弄清楚你定义的cone中哪个锥中的顶点约束，哪个是半径约束。说直白一点就是sedumi函数中的第一个参数应该是
，第三个参数应该是
（第二个参数在我的模型中通常视作0）。
? 和上面的说法相同的还有另一种解释。倘若我们的二阶锥优化模型的标准型定义如下：
?
?
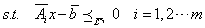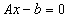其中，?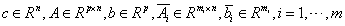
?，而
即是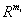
空间中的二阶锥。
? 以上形式定义可以拆分写成另一种，记
第1行为
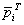，记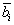
的第1个分量为
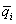，即
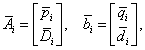所以有：
? 
? 
? 
? 
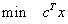
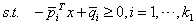
其中，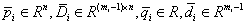
。
?由此可以清楚的辨别，约束表达式中二范数不等式中的A与sedumi软件中设置的参数A有本质的不同了。
