卷积算子优化-2 几种卷积算法

上一篇文章提到了两个优化点，数据重用和重复计算。

这篇文章来学习一下现在卷积常见的几种实现方法。

在直接卷积中，卷积核（滤波器）通过在输入图像上滑动并与图像的每个位置进行逐元素相乘，然后将所有乘积相加得到输出的单个像素值。这个过程可以看作是在输入图像上进行的一种滑动窗口操作，其中卷积核的大小决定了窗口的大小。也就是上一篇文章中提到的C++实现，是一种最朴素的实现，在大部分的情况下表现不如其他算法实现。

最广泛的卷积算法之一就是基于GEMM算法来实现卷积。它包括以下步骤：

将输入转换为一个大矩阵，其中每一列包含在卷积过程中每个滤波器位置所涉及的输入元素。

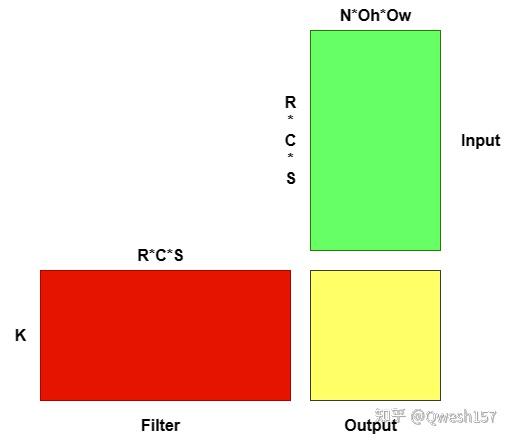
另一个矩阵由每个过滤器的元素生成。最后，卷积的结果由两个矩阵的矩阵乘法（GEMM）提供，如图所示。

转换后的输入矩阵的元素是这样放置的：当GEMM执行一行和一列的标量积时，它将与卷积所执行的标量积相匹配。由于矩阵乘法执行转换后的输入的所有列与转换后的所有行的点积，GEMM操作的结果代表了输入上所有滤波器平移位置上所有滤波器的卷积输出，具体计算过程会在Implicit GEMM小节中介绍。用于获取转换后的输入矩阵的函数通常被称为“im2col”。

由于GPU体系结构的性质和线性代数库中GEMM方法的高效实现，卷积非常适合于放在GPU上计算。然而，这种方法需要大量的内存来存储转换后的矩阵，特别是转换后的输入矩阵，由于卷积中有滑动步长和Padding的存在，转换后的数据矩阵必须存储滑动中重复访问的元素，和一些Padding后额外数据。这在神经网络训练过程中是十分占用显存的，于是就有另一种GEMM实现。

Implicit GEMM是一种用于实现卷积操作的方法，与Img2col+GEMM相似，同样利用了矩阵乘法的性质来加速卷积计算。不同点在于，在内存使用量方面，Implicit GEMM不需要任何额外的存储空间。

在Img2col+GEMM实现中，实现的步骤为：

1.输入输出矩阵转换，用另一块内存空间保存转换后的输入输出矩阵。

2.将输入输出矩阵进行GEMM运算，然后进行输出。

而在 Implicit GEMM中，矩阵转换发生在计算中，也就不需要内存来保存转换后的矩阵，而是在GEMM中进行输入输出的坐标映射，从而实现卷积运算。

在 Implicit GEMM中，主要思想是坐标的映射，怎样使GEMM在load时正确的取到对应坐标元素是关键。参考以下矩阵乘：

for (int i=0; i < M; i++){
    for (int j=0; j < N; j++){
        result[i][j]=0;
        for (int k=0; k < K; k++){
          result[i][j]+=matrix1[i][k]* matrix2[k][j];
        }
    }
}

如果把上图中的Filter作为matrix1，Input作为matrix2，那么GEMM可以变成这样来实现卷积

for (int i=0; i < K; i++){
    for (int j=0; j < N*Oh*Ow; j++){
        output[i][j]=0;
        for (int k=0; k < C*R*S; k++){
          result[i][j]+=filter[i][k]* input[k][j];
        }
    }
}

这个矩阵乘已经可以实现卷积运算，但是注意到Input、Filter和Output并不是二维数据（如果没有经过Im2col转换），这时就要进行坐标变换。

现在假设Input的数据排列格式为NCHW，Filter为KCRS，则输出为NKOhOw，卷积步长为STRIDE。

• Output坐标映射。

按照GEMM来说，Output由i和j两个循环变量决定，则应由这两个变量计算出NKOhOw四个方向的坐标。

    n=j  /（Oh*Ow）                      //N维度坐标
    k=i                                  //K维度坐标
    oh=( j %（Oh*Ow）) / Ow               //Oh维度坐标
    ow=( j %（Oh*Ow）) % Ow               //Ow维度坐标

• Filter坐标映射。

由于为KCRS排列，若把CRS当作一个维度，则Filter可以是一个K行，CRS列的矩阵。此时的循环变量i控制在（0，K-1）内，代表当前处理的是第k个卷积核，k控制在（0，CRS-1）内，代表在当前卷积核内积过程。

    k=i                                  //K维度坐标
    c=k / (R*S)                          //C维度坐标
    r=k % (R*S) / S                      //R维度坐标
    s=k % (R*S) % S                      //S维度坐标

• Input坐标映射。

Input同样有四个维度，由循环变量j和k，还有Filter坐标中的r和s决定。这里的H和W的与当前计算结果的Oh和Ow相关，还有内积过程中的R和S相关。具体公式可表达为：Input.H/W=Output.Oh/Ow * STRIDE - Padding + R/S。则四个维度方向的表示为

    n=j  /（Oh*Ow）                      //N维度坐标
    c=k / (R*S)                          //C维度坐标
    h=oh * STRIDE + r                    //H维度坐标
    w=ow * STRIDE + s                    //W维度坐标

接下来我们重新改写GEMM实现的卷积算法

//Implicit GEMM Convolution

for (int i=0; i < K; i++){
    for (int j=0; j < N*Oh*Ow; j++){
        int on=j/(Oh*Ow);                    //N维度坐标
        int oh=(j%(Oh*Ow))/Ow;               //Oh维度坐标
        int ow=(j%(Oh*Ow))%Ow;               //Ow维度坐标
        output[on][i][oh][ow]=0;
        for (int k=0; k < C*R*S; k++){
            int ic=k/(R*S);                  //C维度坐标
            int ir=k%(R*S)/S;                //R维度坐标
            int is=k%(R*S)%S;                //S维度坐标
            int ih=oh*STRIDE + ir;           //H维度坐标
            int iw=ow*STRIDE + is;           //W维度坐标
            output[on][i][oh][ow]+=filter[i][ic][ir][is]* input[on][ic][ih][iw];
        }
    }
}

Winograd卷积算法是一种用于加速卷积计算的技术。基于Toom和Cook发现的最小滤波算法（Minimal filtering algorithms），Shmuel Winograd在1980年代提出了一类面向卷积神经网络快速算法。

上文中提到了卷积计算可以利用GEMM运算来加速计算，但是GEMM在优化到一定程度以后不再是一个Memory Bound任务，而转变为Compute Bound任务。由于GEMM的计算特性，计算复杂度为O（n^3），一个优化思路就是将运算次数减少。在1969年，Volker Strassen发表了基于分治策略的矩阵乘法算法，算法复杂度降低到O（n^2.81），这个算法也被用来减少卷积神经网络中的卷积次数。而后出现的Coppersmith–Winograd 算法也是用于减少GEMM的计算复杂度，减少到O（n^2.376）。

Winograd算法与上面提到的算法类似，也想通过减少计算次数来提高计算速度。

首先，为了方便表示，用F（m，r）表示一维卷积中Filter内有r个元素，结果有m个。同样的F（m×n，r×s）表示为二维卷积中Filter内有r×s个元素，结果有m×n个，这时Input随着STRIDE等属性有不同的大小。

那么F（2,3）就有

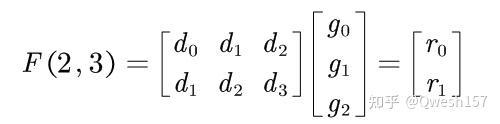
根据最小滤波算法，F（m，r）所需的最小乘法次数为m+r-1，同样的F（m×n，r×s）所需的最小乘法次数（m+r-1）×（n+s-1），更高维度同理。

对上面方法进行复杂度分析，此时的m和n就是之前所提到的Output的Oh和Ow，与Input中的H和W成正比，也就是说从问题规模的角度，卷积的最小乘法次数是与Input的元素数量成正比的。此时为了计算（m+r-1）×（n+s-1）个结果，我们至少要取（m+r-1）×（n+s-1）个值，此时对于每个Input来说，只进行一次乘法操作，达到最优乘法次数。

怎样使乘法次数降低？Winograd通过一系列变换和点乘来实现。以一维卷积为例，有以下公式

其中参数说明：

• g：Filter
• d：Input
• Y：Output
• G：Filter变换矩阵
• ：Input变换矩阵
• ：Output变换矩阵
• ：点积

还是以F（2，3）说明，此时的变换矩阵为

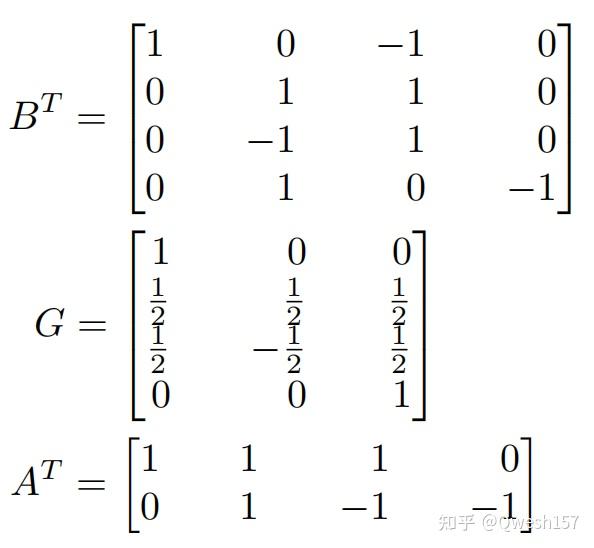
此时又有两个问题，为什么这样可以减少乘法，这个变换矩阵又是怎么来的？（对原理不感兴趣的可以跳过这一部分）

首先，观察卷积F（2,3），Input、Filter和Output 的向量表示

此时若把g和d看做多项式的系数，则两个多项式的乘积为，为了更好的说明多项式乘法与卷积的关系，这里将g向量倒过来（实际上数学定义的离散卷积）

计算后，观察其中 和 的系数，分别为 与 ，为卷积的结果 和

（因为我们的卷积是Filter完全与Input元素对齐后的卷积，所以没算 和 等的系数）。

此时， 的最高次幂为3，则系数为4个， 的系数为3个，而r的最高次幂为3（因为我们定义的卷积是对齐后的）则系数有4个，此时计算r的系数需要6次乘法。若能找到另一种多项式表示方法（替换掉系数表示），使 和 的多项式乘法表达从系数表达变为另一种表达，而后计算的结果再变回系数表达，从而达到减少乘法次数的目的。这个另一种表达，就是接下来要提到的方法，拉格朗日插值法。

根据拉格朗日插值法的定义，这是一种多项式插值方法。拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。因为 有4个系数，那么就是要插4个值。此时 和 的多项式可以分别用拉格朗日插值多项式的四个值来表示。此时多项式乘法变为拉格朗日取值的点积。而后，求出取值的点积结果，后变回系数表达，此时的系数就是我们想要的 。转换矩阵亦可以用拉格朗日插值法求得，具体求法可以参考这里。

此时说明了Winograd的原理后，实现起来非常简单。

以二维卷积F（2×2，3×3）为例，公式如下：

这里的转换矩阵和一维情况相同。由于这样的运算一次能算2×2个结果，所以实现稍稍改变一点。

//Winograd F（2×2，3×3）
float BT[]={ 1,  0, -1,  0 
               0,  1,  1,  0,
               0, -1,  1,  0,
               0,  1,  0, -1};
float G[]={         1,        0,         0,
               1.0f / 2,  1.0f / 2, 1.0f / 2,
               1.0f / 2, -1.0f / 2, 1.0f / 2,
                      0,         0,        1};
float AT[]={ 1, 1,  1,  0,
               0, 1, -1, -1};
for(int n=0;n<N;n++){
    for(int k=0;k<K;k++){
        for(int oh=0;oh<Oh;oh+=2){
            for(int ow=0;ow<Ow;ow+=2){
                //compute r=G * g * GT
                temp=matrixMul(G,filter);
                r=matrixMul(temp,transpose(G));
                //compute s=BT * d * B
                temp=matrixMul(BT,input);
                s=matrixMul(temp,transpose(BT));
                //dotproduct
                y=dot(r,s);
                //compute output=AT * y * A
                temp=matrixMul(AT,input);
                output=matrixMul(temp,transpose(AT));
            }
        }
    }
}

这个实现省去了很多坐标映射和一些计算函数，目的是为了说明Winograd的实现方式，供参考。

首先进行性能分析，上篇文章也提过重复计算的优化，Winograd的性能提升在于乘法次数的减少。以一维卷积F（2，3）为例，乘法次数的减少倍数为 。但是与此同时，Input转换的代价为4次加法，在Filter中若把表达式 看做整体，共需要3次加法，分别是 、 和 ，和 2 次乘法。Output 转换需要 4 次加法。

**Note：在计算机中，两个未知数的乘法代价要高于常数与未知数的乘法。**

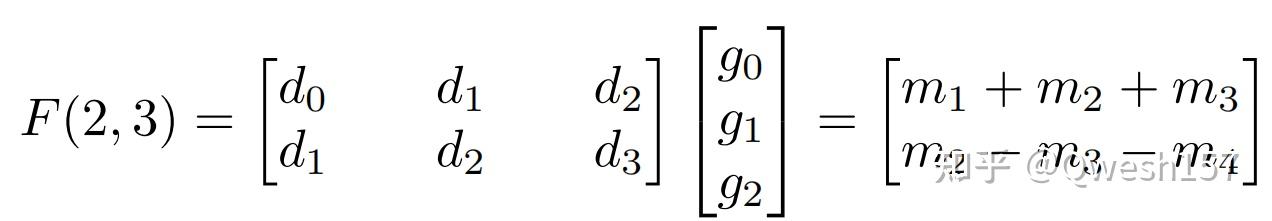
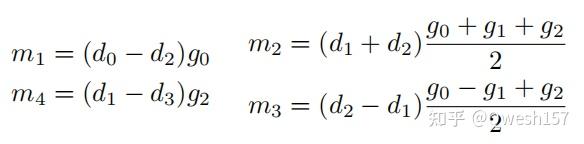
而上升到二维卷积F（2×2，3×3）时，Input转换的代价为32次加法，在Filter中需要32次浮点数操作。Output转换需要24次加法。这里因为编译器会对公共子表达式做一些优化，比如在一维情况下将表达式 看做整体，从而减少浮点数操作。所以具体的代价与转换矩阵有关。

在二维的情况下，Input转换代价相关于 Filter转换代价相关于 Output转换代价相关于

这里可以看出转换代价的提升是与一次运算结果的大小呈二到三次幂相关。那么再来看一下乘法次数的减少倍数

首先，求一下乘法次数减少倍数与一次计算结果个数的相关性。这里将函数对 m、n、r、s 求偏导数即可得出 m 的变化和倍数函数 F 的关系。

可以看出导数恒正，也就是说m、n、r、s越大，乘法次数减少的倍数越大。

但是同时观察这些偏导数，对于 ，进行以下分析：

分子为常数，随着 m/r 的增大，分母变大，导数变小，也就是说在 m/r 变大后倍数变大的趋势变缓。同时这里提到之前所说的代价是与 m、n、r、s 呈二到三次幂相关的。也就是说 m、n、r、s 都不能太大，否则转换的复杂度的增高的代价会远高于乘法减少的倍数带来的性能提升。

同时，假设 m+r 、n+s 为一个定值时，为使倍数 F 变大，F 的分母是常数，也就是 m 和 r 的差异不能太大，n 和 s 同理。在对 Winograd 算法理论分析后，我们得出两个结论：

1. 为尽可能提高计算效率，m、n、r、s 都不能太大，否则转换的复杂度的增高的代价会远高于乘法减少的倍数带来的性能提升。
2. m 和 r 的差值尽可能的小，n 和 s 同理。

在上一小节，提到的 m、n、r、s 都不能太大，否则性能不会有提高甚至性能会下降。也就是说，Winograd 算法不适于大卷积核的卷积，最适用于 Winograd 算法的情况是 3×3 的二维卷积，但是像是 7×7、11×11 的卷积，又或者是三维卷积更适合其他算法。

另一方面，Winograd 目前只用于处理 STRIDE 为 1 的卷积，在其他 STRIDE 下，需要做一些额外处理才能使用 Winograd 。像是 Stride 2 1-D, 2-D, and 3-D Winograd for Convolutional Neural Networks 这篇文章就提出了 STRIDE 为 2 的情况下 Winograd 的应用。

在一维卷积中，将输入和卷积核分为奇数元素和偶数元素后，可将卷积分为两种 STRIDE 为 1 的卷积，此时可以利用 Winograd 对这两种情况进行加速。

而在二维的情况也是类似，将行和列分为奇数行/列和偶数行/列，分为四种情况进行 Winograd 加速。

快速傅里叶变换，也成为FFT算法，是图像处理算法中的相对重要的一部分，该算法是离散傅里叶变换DFT的加速版本(由于本文主要讲解FFT对于卷积的优化，故对该部分不了解的同学请自行搜索)。

DFT的公式如下所示，我们可以对其进行部分变量替代：

我们将e的次幂进行替换： 替换后我们可以得到如下的公式：

假设我们现在有一个数组f为 ，在该数组中的个数应为2的次幂+1个，相对应的我们会有一个离散的傅里叶变换序列 。

对于该离散傅里叶变换序列来说，我们对第k个序列进行计算，计算公式如下：

由于一共有M个这样的数据需要计算，所以对上面的公式进行计算的我们需要M次循环，共计算 次，而此时FFT的优点便可以体现出来了。下面我们将使用FFT对上面的式子进行优化，可以使其只用计算lgM次。

首先我们要将奇数项和偶数项单独提取出来，假设奇数项为 A1 偶数项为 A0 ：

接下来我们需要对 A1 提取公因子：

因此对于F_k来说，就变成了如下所示：

由消去引理可以得到：

易知：

整个过程就是把整体的n个数据转化为2个n/2个数据进行DFT。

但是上面的部分虽然计算速度加快了，但是只计算了序列中的一Fk的DFT，因此我们将引出下面这个公式：

观察可得偶数列系数为正，奇数列系数为负，可以总结出如下公式： 即为只要我们得到其中一个数据的傅里叶变换，通过迭代乘法以单位复数根便可以很快求出整个序列的离散傅里叶变换。

快速傅里叶逆变换(IFFT)与上述过程几乎一样，因此不再过多赘述。python代码实现如下所示： FFT

def FFT(f):
    n=len(f)
    if n==1:
        return f
    w_0=Complex(1)
    f_0=f[0::2]
    f_1=f[1::2]
    y=np.empty(shape=n,dtype=Complex)
    y_0=FFT(f_0)
    y_1=FFT(f_1)
    mid=int(n/2)
    for k in range(0,mid):
        w= Complex(np.cos(-2.*k*np.pi / n), np.sin(-2.*k*np.pi / n))
        y[k]=y_0[k]+w*y_1[k]
        y[k+mid] =y_0[k] - w * y_1[k]
    return y

IFFT

def IFFT(f):
    n=len(f)
    if n==1:
        return f
    w_0=Complex(1)
    f_0=f[0::2]
    f_1=f[1::2]
    y=np.empty(shape=n,dtype=Complex)
    y_0=IFFT(f_0)
    y_1=IFFT(f_1)
    mid=int(n/2)
    for k in range(0,mid):
        w=Complex(np.cos(2.*k*np.pi / n), np.sin(2.*k*np.pi / n))
        y[k]=(y_0[k]+w*y_1[k])/n
        y[k+mid]=(y_0[k]- w * y_1[k])/n
    return y

卷积实际上就是两个多项式的系数进行卷积运算，下面的式子为离散的卷积公式：

在空间域中矩阵的卷积运算，实际上等价于频率域中两个矩阵对应元素相乘，那我们首先将我们需要的卷积运算转换成频率域中的矩阵对应元素乘，便可以进行FFT加速了。

然而我们特征图的尺寸一般情况下要比卷积核的尺寸大得多，如果直接进行FFT变换的话，两个矩阵大小不一样便无法进行对应矩阵乘。因此我们需要对卷积核进行补0操作，使其补充到与特征图的大小相同。由于我们需要补0，所以我们使用FFT进行卷积运算的时候需要选择特征图与卷积核大小相差不多的情况，要不然会由于补0操作造成额外的空间和时间损耗。接下来将以pytorch为例介绍如何构建FFT卷积

1、填充输入阵列

我们需要确保填充后信号和内核的大小相同。 将初始填充应用于信号，然后调整填充以使内核匹配。

# 1. Pad the input signal & kernel tensors 
signal=f.pad(signal,[padding, padding]) 
kernel_padding=[0, signal.size(-1) - kernel.size(-1)]
padded_kernel=f.pad(kernel, kernel_padding)

注意，只在一侧填充内核，因为我们希望原始内核位于填充数组的左侧，以便它与信号数组的开始对齐。

2、计算傅里叶变换

这非常容易，因为在PyTorch中已经实现了N维FFT。 我们只需使用内置函数，然后沿每个张量的最后一个维度计算FFT。

# 2. Perform fourier convolution 
signal_fr=rfftn(signal, dim=-1) 
kernel_fr=rfftn(padded_kernel, dim=-1)

3、乘以变换后的张量

在该部分需要对于张量进行一些处理，具体如代码所示

# 3. Multiply the transformed matrices 

def complex_matmul(a: Tensor, b: Tensor) -> Tensor: 
    """Multiplies two complex-valued tensors.""" 
    # Scalar matrix multiplication of two tensors, over only the first two dimensions. 
    # Dimensions 3 and higher will have the same shape after multiplication. 
    scalar_matmul=partial(torch.einsum, "ab..., cb... -> ac...") 

    # Compute the real and imaginary parts independently, then manually insert them 
    # into the output Tensor.  This is fairly hacky but necessary for PyTorch 1.7.0, 
    # because Autograd is not enabled for complex matrix operations yet.  Not exactly 
    # idiomatic PyTorch code, but it should work for all future versions (>=1.7.0). 
    real=scalar_matmul(a.real, b.real) - scalar_matmul(a.imag, b.imag) 
    imag=scalar_matmul(a.imag, b.real) + scalar_matmul(a.real, b.imag) 
    c=torch.zeros(real.shape, dtype=torch.complex64) 
    c.real, c.imag=real, imag 

    return c 


# Conjugate the kernel for cross-correlation 
kernel_fr.imag *=-1 
output_fr=complex_matmul(signal_fr, kernel_fr)

4、计算逆变换

同样直接使用pytorch库函数即可

# 4. Compute inverse FFT, and remove extra padded values 
output=irfftn(output_fr, dim=-1) 
output=output[:, :, :signal.size(-1) - kernel.size(-1) + 1]

5、添加偏置值并且返回

这一步是卷积中的加偏置项的操作，就是一个简单的加法

# 5. Optionally, add a bias term before returning. 
if bias is not None: 
    output +=bias.view(1, -1, 1)

文章有什么错误的地方欢迎各位指出^_^

Implicit GEMM：

MegEngine TensorCore 卷积算子实现原理 - 知乎 (zhihu.com)

cutlass/media/docs/implicit_gemm_convolution.md at main · NVIDIA/cutlass (github.com)

Winograd转换矩阵求法：

Winograd算法的数学推导

Winograd、拉格朗日插值法原理参考：

【人工智能芯片入门】卷积、对偶性、与Winograd算法_哔哩哔哩_bilibili

【拉格朗日插值法的本质】

Fast Algorithms for Convolutional Neural Networks

Stride 2 1-D, 2-D, and 3-D Winograd for Convolutional Neural Networks

PyTorch中的傅立叶卷积：通过FFT有效计算大核卷积的数学原理和代码实现

傅里叶变换、离散傅里叶变换(DFT)、快速傅里叶变换(FFT)详解

卷积神经网络之快速卷积算法(img2col、Winograd、FFT)：